What Is a Sandwich?

Using lots of philosophy and math to answer a silly question

I have a special place in my heart for the perennial online debate over whether a hot dog is a sandwich. I enjoy all sorts of low-stakes online arguments, but the sandwich debate helped me realize something important about definitions. Once while reading one of these debates I tried to use a list of foods I considered sandwiches and non-sandwiches to come up with a precise definition of a sandwich. But I realized that any simple definition I tried had obvious counterexamples, and after adding a few epicycles and still not reaching a satisfying definition, I decided that no simple yet complete definition existed for sandwiches, and probably for many other things as well.

Unbeknownst to me at the time, Ludwig Wittgenstein had already said some very clever things on this topic in his book Philosophical Investigations while defining games. He brings up a number of characteristics games often share, noting that none of these features are universal among them. Instead he compares the similarities between games to family resemblances:

I can think of no better expression to characterize these similarities than "family resemblances"; for the various resemblances between members of a family: build, features, colour of eyes, gait, temperament, etc. etc. overlap and criss-cross in the same way.— And I shall say: 'games' form a family. And for instance the kinds of number form a family in the same way. Why do we call something a "number"? Well, perhaps because it has a—direct—relationship with several things that have hitherto been called number; and this can be said to give it an indirect relationship to other things we call the same name. And we extend our concept of number as in spinning a thread we twist fibre on fibre. And the strength of the thread does not reside in the fact that some one fibre runs through its whole length, but in the overlapping of many fibres.¹

Wittgenstein further argues that there is no natural sharp edge to concepts based on family resemblance, although we can draw boundaries if we need to.

Inspired by Wittgenstein’s ideas, I decided to test out whether I could use a simple model of family resemblance to mathematically predict the “sandwichness” of various foods using some help from Anthropic’s Claude Sonnet 3.5². First, I asked Claude to give me a list of 100 different foods, including some clear sandwiches and non-sandwiches, as well as some edge cases. Then, I put together a list of sandwich family traits. I decided to make sandwichness and all of the traits continuous variables bounded between 0 and 1. The first three traits below are based on the definition of a sandwich from Wikipedia, and the rest were suggested by Claude:

• Sandwich: The "sandwich-ness" score, ranging from 0 to 1.

• Filling: Presence and prominence of a filling (0 to 1).

• Slices: Use of distinct bread slices (0 to 1).

• Wrapper: Presence of a wrapping or enclosing element (0 to 1).

• Handheld: Ease of eating by hand (0 to 1).

• Layered: Degree of layered construction (0 to 1).

• Bread_prominence: Importance of bread or bread-like component (0 to 1).

• Customizability: Ease of customizing or modifying (0 to 1).

• Cold_served: Likelihood of being served cold or at room temperature (0 to 1).

Next, I asked Claude to create a csv that assigned values for each variable to each of the 100 foods. To make sure values it produced were consistent, I had Claude do this five times, and took the median value. For sandwichness, the numbers assigned were quite consistent between rounds, with no foods having a maximum difference of greater than 0.3. Some other variables showed more differences, but none were consistently bad. Here’s what the median assignments look like for the first 25 foods³:

In most cases, foods that I think of as more sandwichy get higher sandwichness scores here, though many of the values are quite high! I would not call a burrito or a corn dog a sandwich, but they got scores of 0.7 and 0.6 respectively. I separately asked Claude to assign simple yes/no values to whether each of the foods was a sandwich, and for all foods that had scored 0.8 and above it said yes, and for nearly all at 0.7 or below, it said no. So one reasonable place to draw a boundary between sandwiches and non-sandwiches would be around 0.75. But as Wittgenstein assures us, it’s okay if we leave the boundary fuzzy as well.

So is a hot dog a sandwich then? It’s a close call, Claude assigns it 0.7. That’s just below the arbitrary cutoff I just assigned, so I lean very slightly no, but the fact that it’s an edge case is probably part of why it sparks such lively debate.

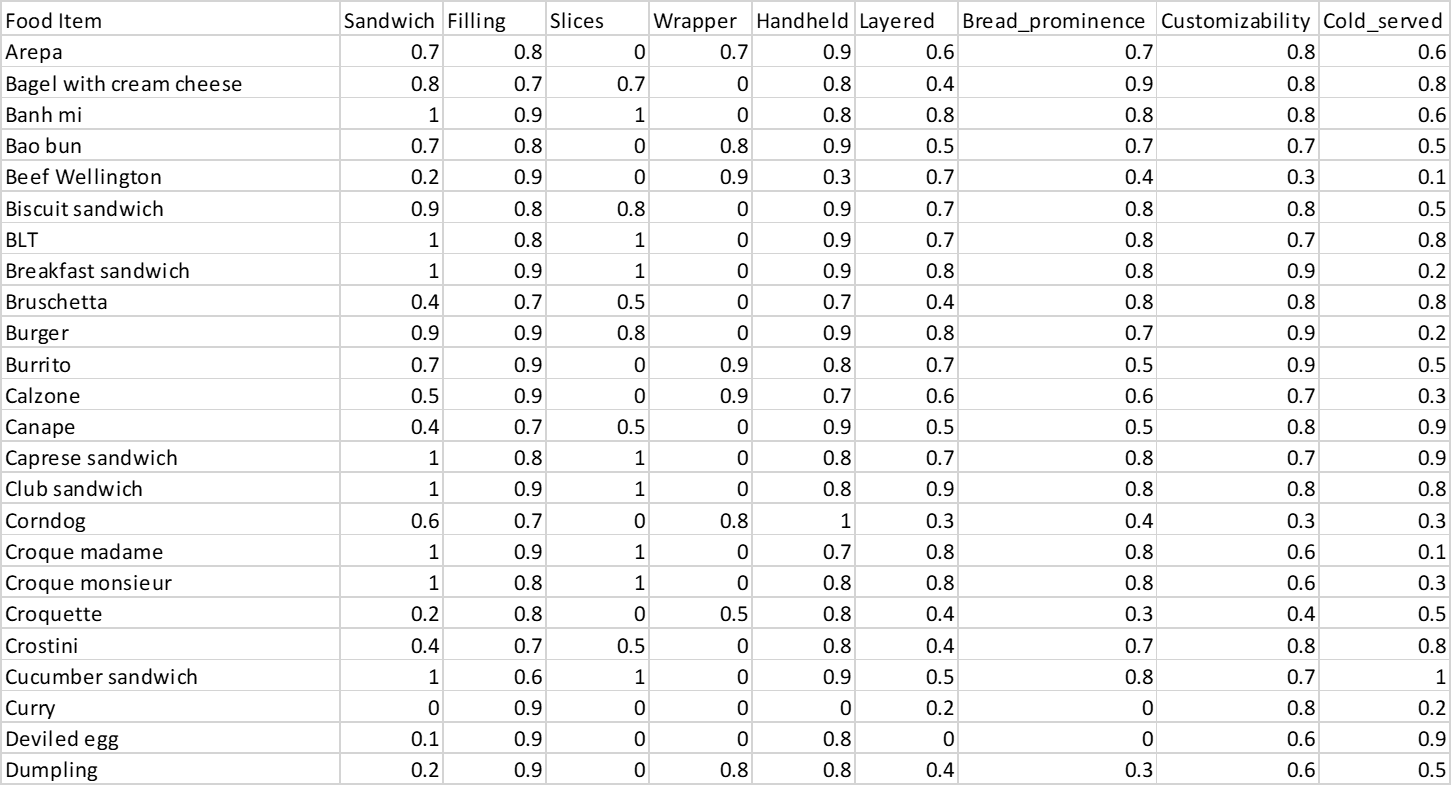
I used the data Claude provided to run a plan old linear regression in R. It’s not a perfect method since it can produce fitted values that are outside the [0,1] range I’ve assigned for sandwichness, but it’s nice and easy to interpret, and a fractional logit model didn’t perform much better. Filling, Wrapper, and Cold_served weren’t statistically significant and had trivial effect on fit, so I dropped them. Here are the final results of the regression:

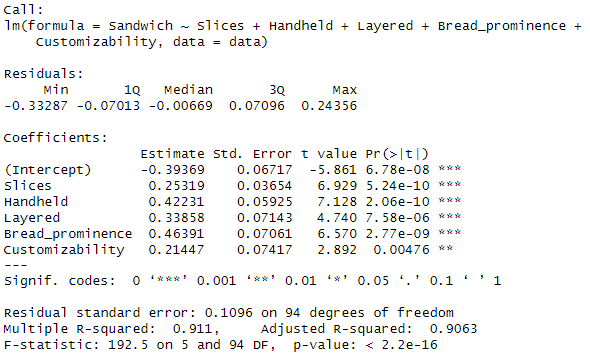
These characteristics all seem to influence sandwichness to a similar degree, with breadedness and handholdability being the largest factors. Here are the sandwichness values Claude produced compared to the fitted values based on the model.

This fit seems pretty good, especially considering that there are probably important sandwich characteristics I didn’t include, and that the effect of the characteristics probably isn’t linear like I’ve assumed. Recall that around 0.75 is around where we might start to call something a sandwich if forced to choose. The model says that soup is the least sandwichy food, and a panini is the most sandwichy. French toast is the biggest outlier, though I partly blame Claude for making the questionable decision to assign it a 0.7 value for Handheld.

I’m not sure whether this analysis tells us very much about language. It seems consistent with Wittgenstein’s family resemblances, though I think the model of sandwichness we have in our heads probably works quite differently from this. But the reasonable fit does make me feel good about Claude’s ability to map characteristics to a numerical scale. I’m excited to to explore that more, I expect it has some interesting and maybe even useful applications.

If you have any suggestions you’d like me to try, let me know and I’ll happily test them out. I’ve also put my data, code, and Claude prompt in a Google Drive folder here. That folder also has a Python Script I made (ok, that Claude made) after the fact that makes generating the data more automated and flexible.

I’d like to thank Matthew Adelstein of Bentham’s Bulldog for his post Lots of People Don't Know What a Woman Is for helping me think about this topic.

1. Ludwig Wittgenstein, Philosophical Investigations, Section 67. I recommend reading the whole section on defining games, Sections 65-71

2. I mention Claude quite a few times in this post, and with good reason. It (I have to force myself to say it and not he) has been helpful not only in generating data for me, but in acting as a philosophy tutor as well. It was Claude that pointed me to Wittgenstein’s writing in response to me asking about fuzzy concepts.

3. Here’s the full list: